2.2 Ocular velocity versus measured velocity
It is a common misconception that nothing can be seen to travel faster than the speed of light. What should instead be meant is that no object can appear to travel faster than 1c when it is measured from another frame of reference. Ocular velocity is an important aspect of the verification of true relativity, and it can certainly exceed 1c by any amount.
Let us say that two planets are located 10 lm (light-minutes) from each other, and let us send an object from planet A to planet B. The planets are aware of their spatial delay, and when they discuss the measured travel time of the object, they will agree that it took 20 minutes for the object to travel the 10 lm. The measured speed is 0.5c.

If the object were large enough to be optically seen at such a distance, planet B would see the object stand still for the first 10 minutes of the experiment, approach at a speed of 1c and then arrive at the planet after another 10 minutes. Planet A would see the object moving at 0.333c and arrive at planet B after 30 minutes because the ocular event of the landing also requires 10 minutes to reach planet A.
When calculating the ocular velocity, one must take the spatial delay into account by adding it to the travel time on the departure side and by subtracting it from the travel time on the arrival side.
|
Measured travel time |
1000 min |
100 min |
20 min |
15 min |
12 min |
|
Measured velocity |
0.01c |
0.1c |
0.5c |
≈0.667c |
≈0.833c |
|
Ocular travel time acc. to A |
1010 min |
110 min |
30 min |
25 min |
22 min |
|
Ocular velocity according to A |
≈0.010c |
≈0.091c |
≈0.333c |
0.4c |
≈0.455c |
|
Ocular travel time acc. to B |
900 min |
90 min |
10 min |
5 min |
2 min |
|
Ocular velocity according to B |
≈0.011c |
≈0.111c |
1c |
2c |
5c |
Apparently, there is no limit to the ocular velocity observed from planet B. The object can be seen to move at any speed, but the initiation of the movement of the object is always delayed by 10 minutes. Regardless of how much energy is conferred to the object, it will always require at least some time to travel in addition to the 10-minute spatial delay. The ocular velocity observed from planet B approaches infinity when the measured velocity approaches 1c.
(Remember that an object travelling rapidly toward the observer will appear to be blueshifted. At extremely high speeds, visible light from such objects will become gamma rays, and the term "see" must include "being able to detect electromagnetic waves of any frequency".)
The equation used to transform the ocular approaching velocity (βoa) into the measured velocity (βm) can also be used to transform the measured velocity (βm) into the ocular departing velocity (βod).
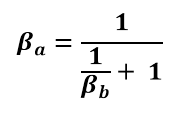
The above equation implies that βa is less than βb. To transform the velocities back, the reverse equation is used:
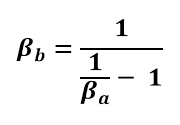
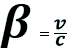
β is the velocity in units of c – in units of the spatial delay. β is a universal variable, independent of how we have decided to measure time and space. It is used throughout the description of the MRM to minimize the use of the human-defined constant c.
The following table summarizes the results of such transformations for various velocities:
|
βoa |
βm |
βod |
|
0.001 |
0.000999 |
0.000998 |
|
0.01 |
0.0099 |
0.0098 |
|
0.1 |
0.091 |
0.083 |
|
0.2 |
0.167 |
0.143 |
|
0.25 |
0.2 |
0.167 |
|
0.3333 |
0.25 |
0.2 |
|
0.5 |
0.3333 |
0.25 |
|
1 |
0.5 |
0.3333 |
|
2 |
0.667 |
0.4 |
|
5 |
0.833 |
0.45 |
|
100 |
0.99 |
0.4975 |
|
1000 |
0.999 |
0.499975 |
It should be noted that with increasing velocity,
- βoa approaches infinity,
- βm approaches 1 (the spatial delay) and
- βod approaches 0.5 (half the spatial delay).