3.8 The profound nature of movement

According to the MRM, time is an effect arising from infinitesimal interactions. Due to this postulate, time must be described as an accumulated result due to immediate changes. The MRM entirely focuses on immediate changes. Movement must thus originate from the formula derived in section 3.1 The Internal Geometry Shift (IGS). The formula becomes somewhat clearer if we use the definition of proper velocity u = γβ.

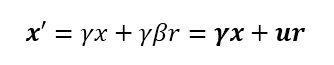
$The IGS transformation$

This formula represents a three-dimensional transformation because r describes the total distance to a location, taking all three axis; x, y and z , into account.

I. Let us study a two-dimensional situation. A compound is stationary with respect to its surroundings. The total momentum of the compound is 0 because that is the sum of all momentum vectors.

Mass: If we regard the magnitude of each momentum vector in I as being 1 in any arbitrary unit, the compound has a mass of E_int = 8 in that arbitrary unit. P = E for each single momentum vector.

II. The compound is accelerated to u = 1. The compound will now experience a change in geometry as described by the IGS. The total momentum of the compound is still 0 because the image shows how geometry is interpreted by the compound itself. Compounds always regard themselves to be stationary - to have a balanced momentum.

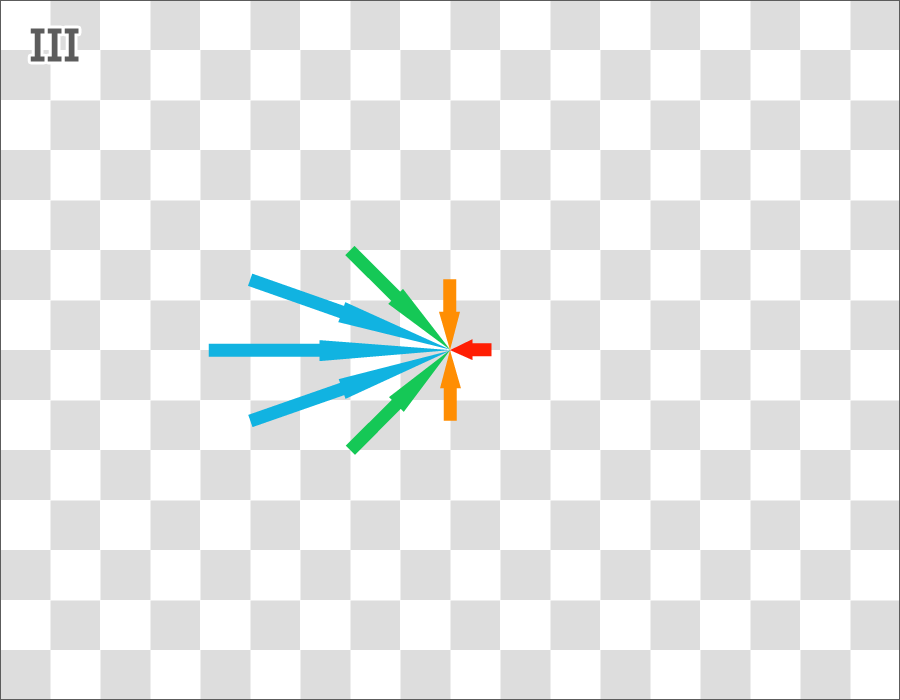III. This image shows how the stationary frame of reference interprets the change in momenta inside of the compound. The IGS transformation is applied on the base of vectors in the opposite direction, x' = γx - ur.

Momentum: If we use vector addition for all momenta in III, it will produce a result of 8 to the right. This is the total momentum arising from the formula P = E_int u, where E_int = 8 and u = 1.

Kinetic energy: The energy required to produce this change in momentum can be calculated by adding up the magnitudes, the lengths, of all vectors, independent of direction. In I, the sum is 8. In III, the sum is 11.314, meaning the acceleration required an extra energy of 3.314. This result is consistent with E_ext = E_int(γ - 1).

Mathematically, it is convenient to use these star-shaped symbols to perform transformations of momentum vectors. In real compounds, the momenta, the energy vectors, are in a constant buzz. They move at the "speed of light", the delay of the time filter, continuously exchanging momentum with each other. When this buzz becomes tilted, it makes objects move according to each other. This is the profound nature of movement.

To explore the effect of movement, we can imagine two momenta rotating around each other - two "photons" being attached to each other. The MRM does not directly suggest that such constructions can form, but it is mathematically coherent with any form of buzzing and exchange of momentum between momenta. Mathematically, two momenta are just sufficient to form a relative velocity.

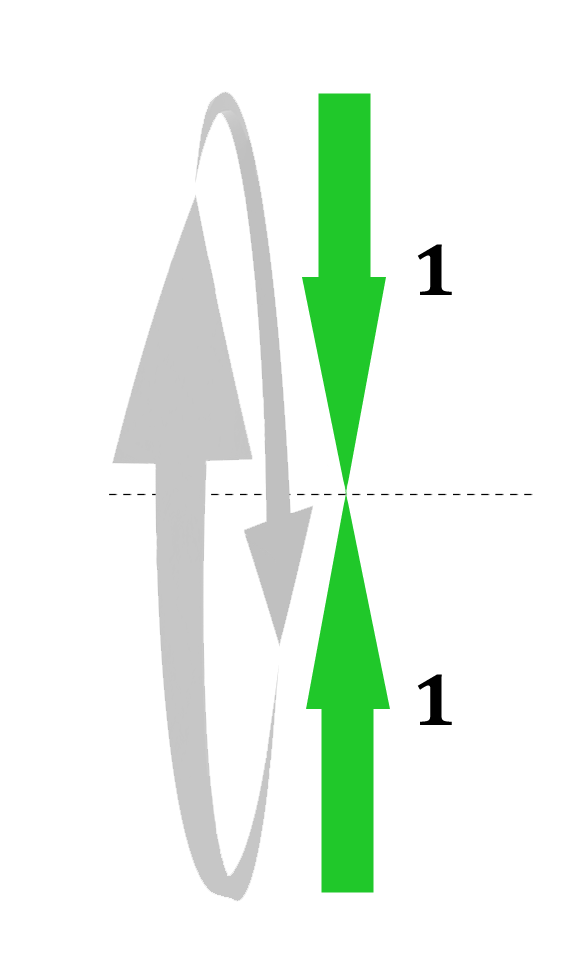The simplest visualization of profound movement is to imagine two momenta that are rotating around each other. They are located at x = 0, rotating around the x-axis, into the paper or the screen. The two momentum vectors have equal size; let's say their energy, their magnitude, is 1 in any arbitrary unit. The compound as a whole has thus an internal energy (mass) of E_int= 2 in that arbitrary unit, and it remains stationary according to us.

If we want to accelerate the compound to the right, the IGS transformation tells us that the base of the momentum vectors should be transformed by x' = γx - ur. In this case, x = 0 and r = 1, which means that x' = -u. This fact makes this particular configuration easy to examine.

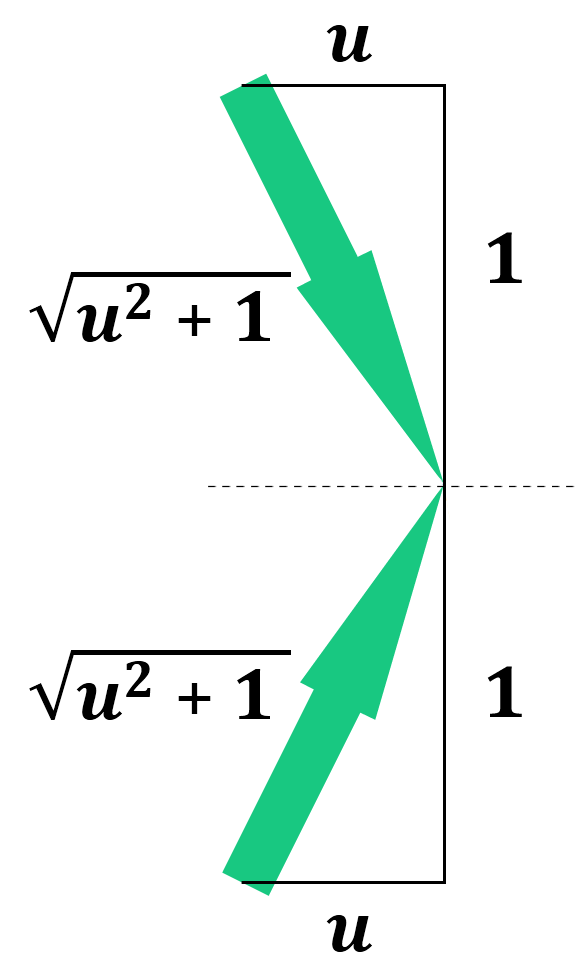The total energy required for acceleration is equal to the change in the total magnitude of vectors, their total length, regardless of direction. For a single momentum, we see that the length of the final vector will end up being 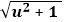using the Pythagorean Theorem. The change in energy is thus 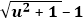, which should be multiplied by 2 for both vectors:
E_ext= .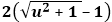

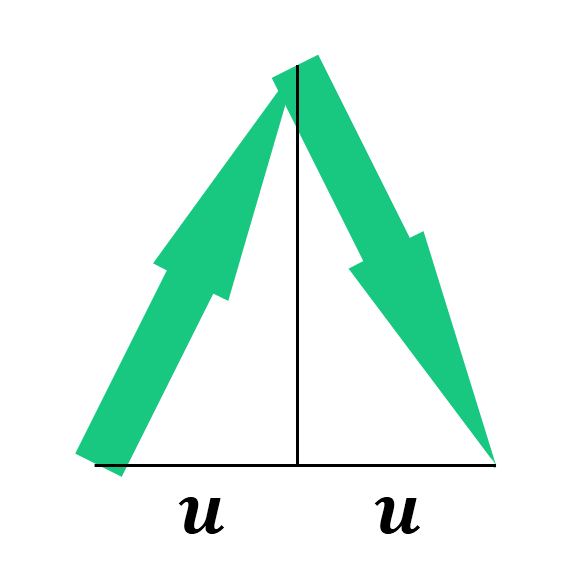The total momentum is the sum of all vectors. In this particular case the x-position of the base of each vector changes by the amount of u. The total momentum will thus be P = 2u to the right.

When the momenta spin in their new direction, they propel the accelerated compound forward through our frame of reference. This is the profound nature of movement.

The time required for each rotation has increased by a factor of 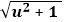(=γ) because the momenta now have this longer way to travel according to us. This is not due to time dilation. According to the view of the MRM, this is the cause of time dilation.

Now, let us examine two momenta rotating around the z-axis. Both have a magnitude of 1 in any arbitrary unit, and the compound as a whole has thus an internal energy (mass) of E_int= 2. The momenta have a continuous exchange of momentum, meaning their sum in momentum always is 0.

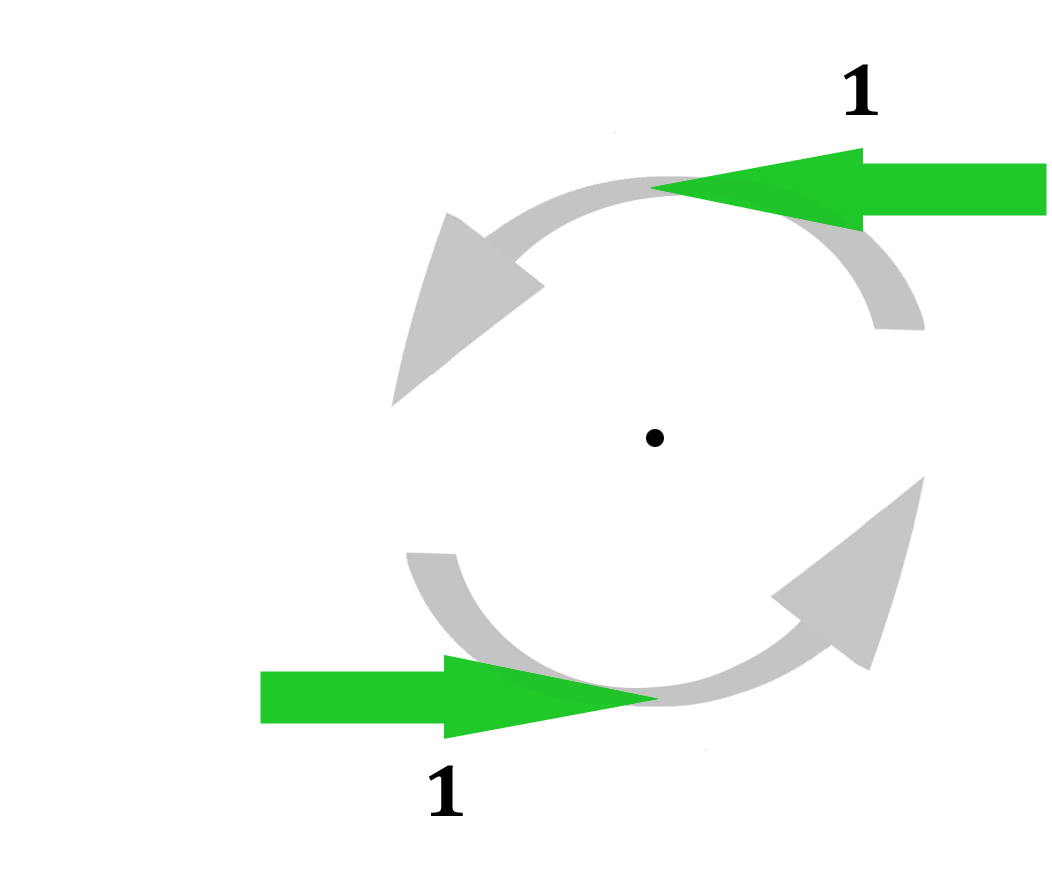
If we now want to accelerate this compound to the right, the IGS transformation tells us that the momentum vectors should be transformed by x' = γx - ur. In this particular case, x₁= 1, x₂= -1 and r = 1, which means that x₁' = γ - u and x₂' = -γ - u. The length of the second momentum vector is thus | -γ-u |= γ + u.

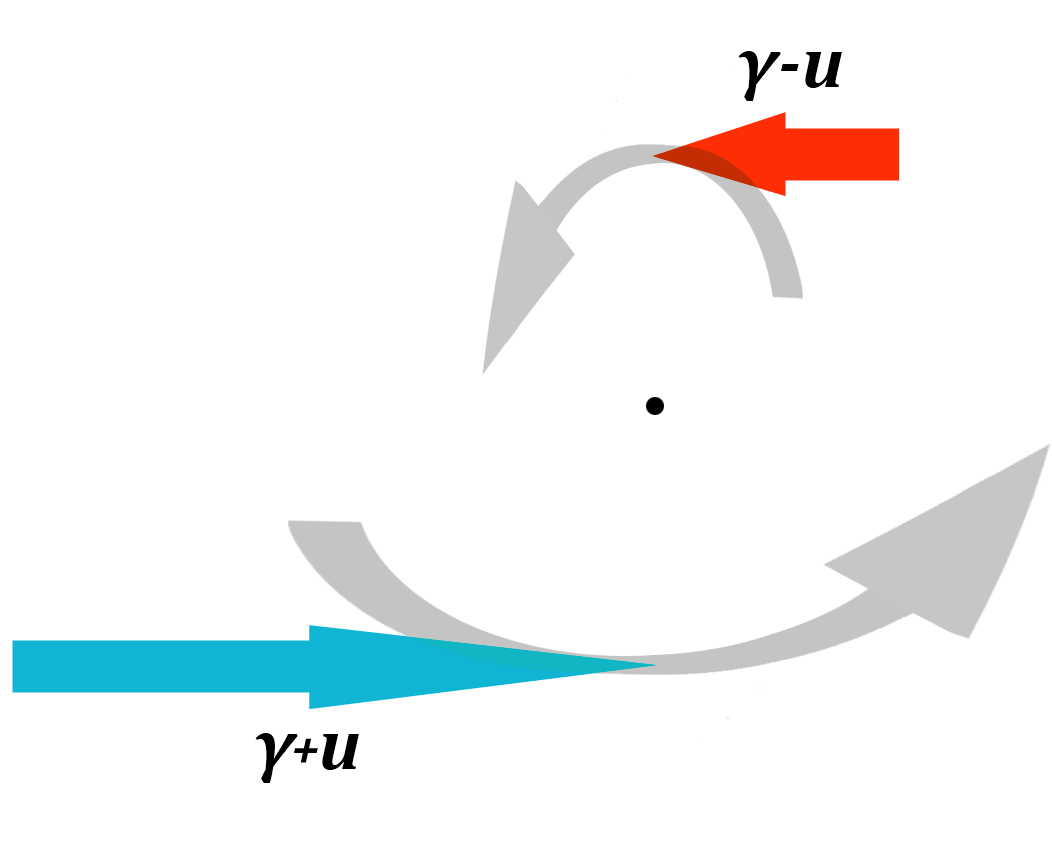The total energy required for acceleration is equal to the change in the total magnitude of vectors, their total length, regardless of direction. In this particular case the x-values of the two momenta are their entire magnitude, which means that E = γ - u + γ + u = 2γ. Before acceleration, the two momenta had a total length of 2. The acceleration thus required an extra energy of E_ext= 2γ - 2 = 2(γ - 1) = .

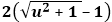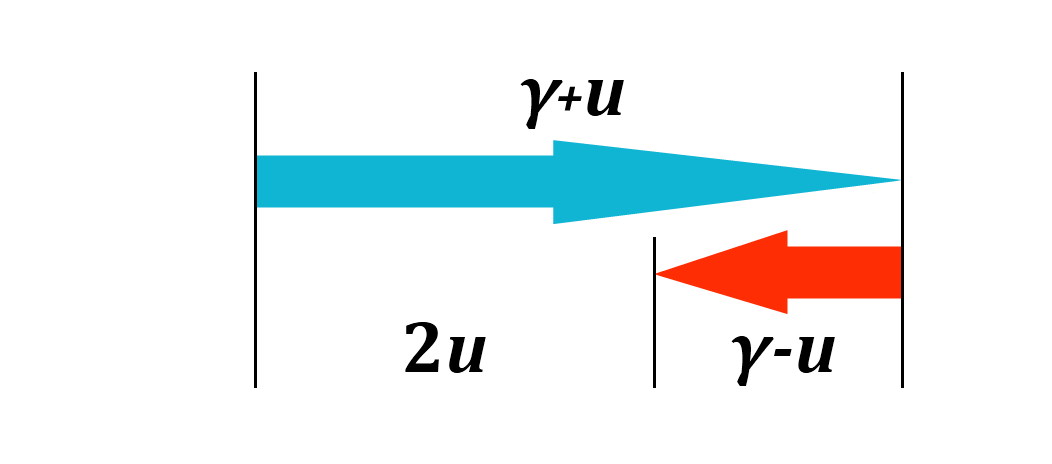The total momentum is the sum of all vectors. In this case,
P = γ + u - (γ - u) = 2u to the right.

When the momenta continuously exchange momentum, they propel the accelerated compound forward through our frame of reference.

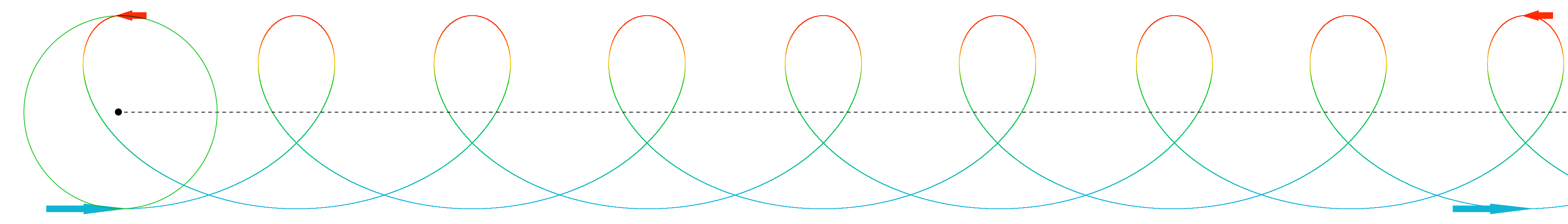
We have examined two of the simplest examples, but it is possible to apply the IGS transformation on any number of momenta, with any directions and magnitudes, as long as they have a total momentum of 0 before the acceleration, and one will see that

E_ext= E_int (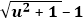) always describes the total extension of magnitudes and that
P = E_int u always describes the total vector sum.

To summarize all relativistic effects, one can conclude that the IGS is the source of two compounds'

relative angular aberration,
relative velocity,
relative time dilation,
relative length contraction,
relative kinetic energy
and relative momentum.

The total energy attributed to a compound according to a frame of reference is defined as E_int + E_ext = E, where MRM suggests that terms are used as follows:

E_int is the mass of the compound.
E_ext is the kinetic energy of the compound according to a frame of reference.
E is the total energy attributed to a compound according to a frame of reference.

These definitions are compatible with the concept of invariable mass.

It all comes down to what we want to include in the word mass. If we want to use the concepts of relativistic mass and rest mass , such as in SR, terms would be used as follows:

E_int is the rest mass of the compound.
E_ext is the kinetic energy of the compound according to a frame of reference.
E is the relativistic mass of the compound according to a frame of reference.

The concept relativistic mass simply replaces the word energy. The question is what it pedagogically is intended to explain. Relativistic mass includes both the rest mass and the relative kinetic energy. The unit independent formula for momentum according to such view is P = E β. It makes it harder to conceptualize the interconnection between the vector additions and the result of P, but it has the advantage that one quite easily can calculate the relative velocity (β) of objects by adding all vectors (P) and then dividing the result by the total magnitude of all vectors (E). This calculation illustrates what was stated in 1.1.3 Interactions: the "relative average" of all internal momentum vectors within compounds determines the compounds' relative velocity.

It is not possible to use the formula P = E_int u to calculate relative velocity directly from vectors because it requires that we first transform the vectors back to find E_int. To do this transformation, we have to know the velocity u, the value that we want to calculate.