4.1 The External Geometry Shift (EGS)
4.1.3 EGS formulae
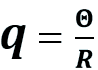
The objective of using this three-component solution is to minimize the use of human-defined units in gravitational equations.
Θ and R represent distances and must be specified in the same units. Any unit can be used: light-years, light-seconds, meters, femtometers etc.
Θ represents the size of a spatial cavity (gravitational field). Specifically, Θ represents the radius of the cavity edge when this radius is defined as a distance in the flat parent space. If the mass M of an non-rotating body is known, then Θ can be calculated in units of light-seconds using traditional constants: Θ = GM/c3 (or, in meters, Θ = GM/c2 ).
R represents an altitude within a spatial cavity and must be specified in the same units as Θ. It is also possible to specify R directly in units of Θ. The cavity edge is located at R=1Θ.
q represents an altitude within a spatial cavity. Specifically, q is the ratio of Θ and R. It is unitless and increases with increasing depth. The cavity edge is located at q=1.
q can be obtained directly using traditional units and constants: q=GM/rc2
Within a gravitational field, all momentum vectors are affected in accordance with
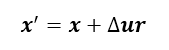
when calculating the change in the base of the vector, or
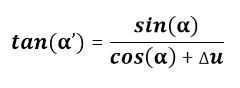
when we only want to know the angular change and not the changes in magnitudes.
Δu represents an infinitesimal change in velocity in the direction (the x-axis toward a compound of energy (mass).
The experienced magnitude of this velocity change depends on frame of reference, but it can in general be defined as Δu = Θ/R2 during the length unit (time) used for Θ and R
or Δu = GM/r2 per meter (1/299,792,458th of a second) using traditional units and constants.
The cavity edge is located at q = 1 or, in units of meters and using traditional units and constants, r = GM/c2.
The cavity edge should not be confused with the event horizon of GR. The MRM does not support the existence of an event horizon because the direction of a momentum vector cannot be reversed by a change in speed. Momenta can only become bent or change in energy level.
The conclusions of the MRM must differ from what is described by GR. According to the MRM, there is always an exit point from the cavity. Energy, such as light and matter, is not unconditionally trapped inside such a cavity, but in a deep cavity, it will be less likely for free momenta to escape because the parent space has been reduced to a small exit in the new cavity. Moreover, any momenta that exit a deep spatial cavity are likely to be extremely redshifted.