4.4 Energy relations in gravitational systems

As observed in a previous section, an object obtains a proper speed of 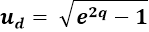when falling from rest at an infinite distance into the cavity. This theoretical observation can be combined with the principle of the conservation of energy, resulting in a formula for gravitational potential energy written as
- E_int(e^q - 1).

The gamma factor between the withstanding and default falling frame of reference is written as e^q, and so is the size contraction.

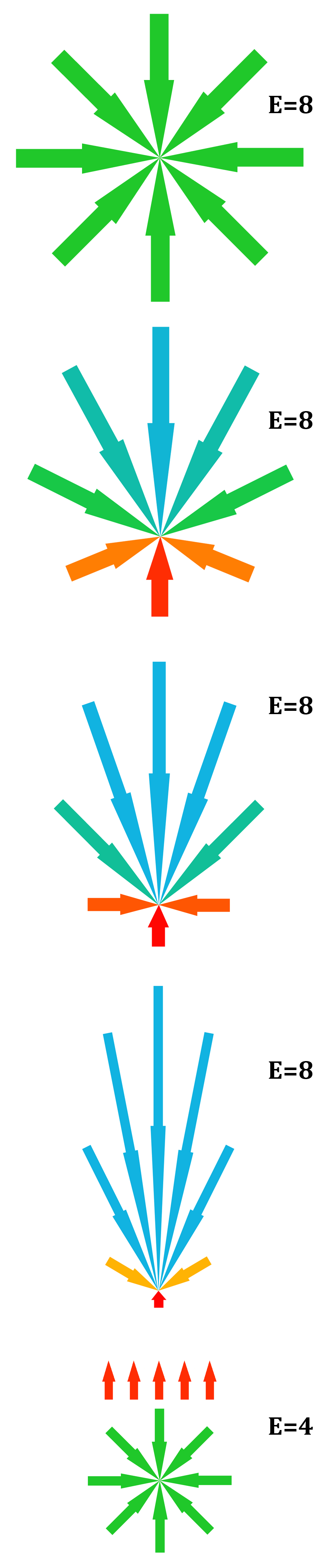
These conclusions are very useful when examining the change in momentum vectors within compounds. We can see that as the compound gains speed, the total value of the vectors decrease by an amount of e^q due to the size contraction. Therefore, no energy is neither added nor removed from the compound. The total magnitude of all vectors stays constant. Gravitation only redistributes the momenta that are already present in the compounds.

An object being located outside of the gravitational system of a planet is thus slightly larger than an identical object standing on the ground of the planet. The momenta in the object in space is worth more than the one standing on the ground. If the object in space starts to fall toward the planet, this larger momenta will be redistributed to become unbalanced in relation to the ground. When the object hits the ground, the excessive energy must disappear in some way. If the excessive energy radiates back into space, the object will now be slightly smaller, and it will contribute to a smaller amount of the entire θ of the gravitational system than what was expected when the object was floating in space.

If the object does not stop, its total energy will be retained, and it will contribute to the total θ of the system with its entire energy.