4.2 Time dilation
4.2.2 Derivation
To calculate the time dilation for the withstanding frame, we can use the falling frame as the reference. By definition, we know that an object that is stationary at an infinite distance outside of the gravitational system will not be time dilated with respect to an object that has expanded from that position, thereby moving into the cavity. Based on this theoretical observation, we can imagine a default velocity at each position within the cavity. To find the time dilation factor at each altitude, we must thus first derive this default velocity at each altitude.
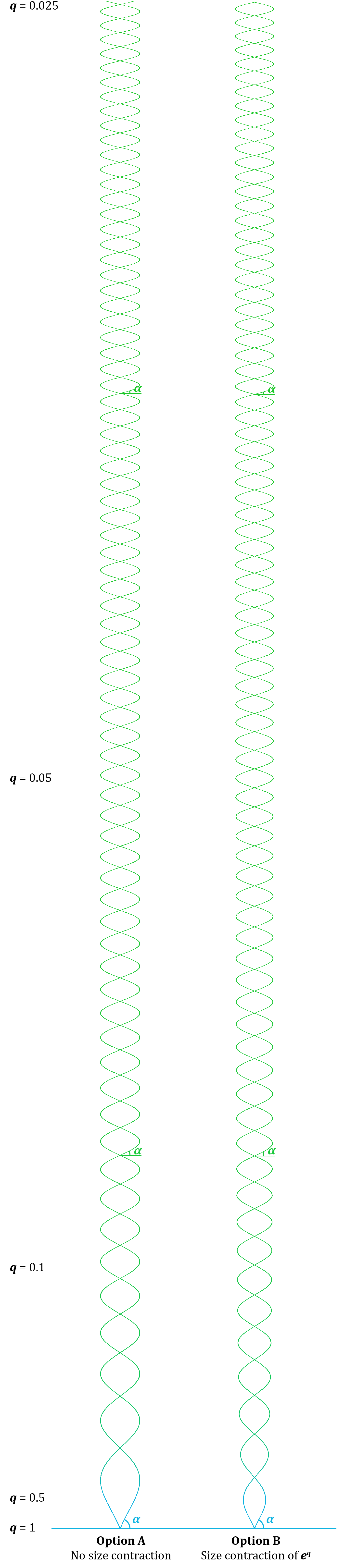We can drop two rotating momenta (the same theoretical compound was used in 3.8. The profound nature of movement) into a geometric system defined by the EGS and simply see what happens. Ray tracing and analysis of the resulting angles (α) show that the default velocity must be defined as:
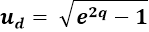
The withstanding frame must therefore observe itself to constantly travel within the synchronized expanding space at this proper velocity. To describe the time dilation, we can calculate the Lorentz factor from its relation to the proper speed:
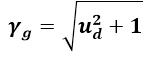
yielding an MRM gravitational time dilation factor of:
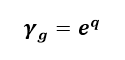
The formula for gravitational time dilation according to the MRM is not consistent with the GR gravitational time dilation factor, which can be written as:
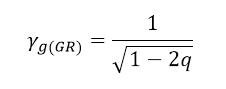
As long as q is 0.01 or less, the two models will produce approximately the same result. As we approach the cavity edge, the results will begin to differ radically between the models.
The simulation appears more consistent and logical if we contract the compound sideways by an amount of eq (option B), especially at very low altitudes. If the falling frame of reference is synchronized, each revolution of the rotation must take the same time. Either momenta, including light, moves much faster in the downward direction, as in option A, or space is contracted, as in option B.
In option A, the change in proper velocity for the default falling frame is
,
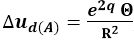as the falling objects receive more geometrical changes when they move through the geometry at this high speed.
In option B, the change in proper velocity for the default falling frame is
.
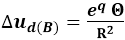The worth of the accumulated velocity ud, however, does also decrease by a factor of eq. Objects fall for a longer period of time, thus accumulating the same velocity ud as in option A.
(Note that the expression "change in proper velocity" above does not imply a perceived acceleration. Falling objects do not experience any acceleration.)
Both option A and option B seem to be mathematically possible. In the coming sections, a number of reasons why option B is more feasible will be elaborated.