4.3 Size contraction

4.3.2 Derivation

To obtain a formula for the gravitational size contraction, or gravitational space expansion if seen from the inner reference frame, we must turn to geometrical properties.

Let us imagine a very narrow triangle in a gravitational field. One side (A) of the triangle is leading straight out of the cavity. The smaller side (B) could be of any length but must be short in relation to line A. The angle for the diagonal (C) is found so when it is ray traced using the EGS, it meets the center of the cavity from the same direction as line A. Line C approaches line A, but it never crosses it. For reasons elaborated later, there may not exist actual singular centers in cavities (where q approaches infinity), but one could expect the geometry in gravitational systems to be consistent with a situation where they could exist.

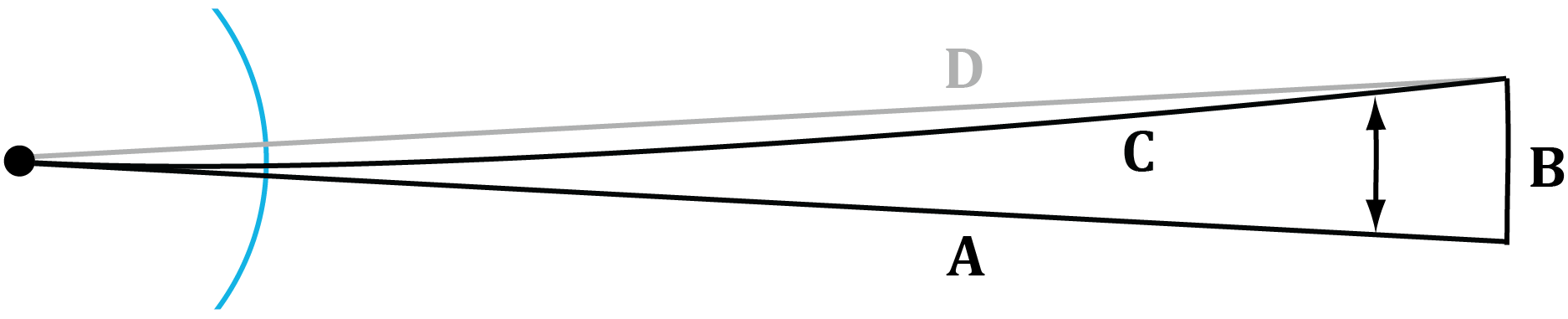
Now we ray trace and plot the distance between line A and line C at every altitude. We find that the ray traced distance at every q perfectly matches the curve of 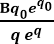 , where q₀ is the q-value at the location of B.

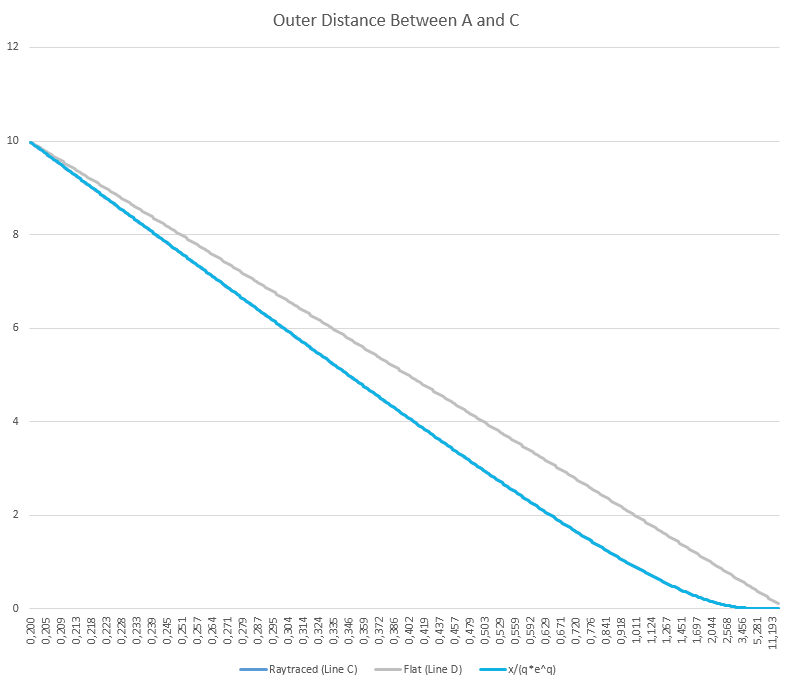
It is possible to zoom in at any altitude to confirm that this assertion is correct.

As 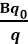is expected in a flat space (the distance between line A and line D), we can conclude that gravitational systems seem to expand space by a factor of e^q , the inverse of the natural logarithm.

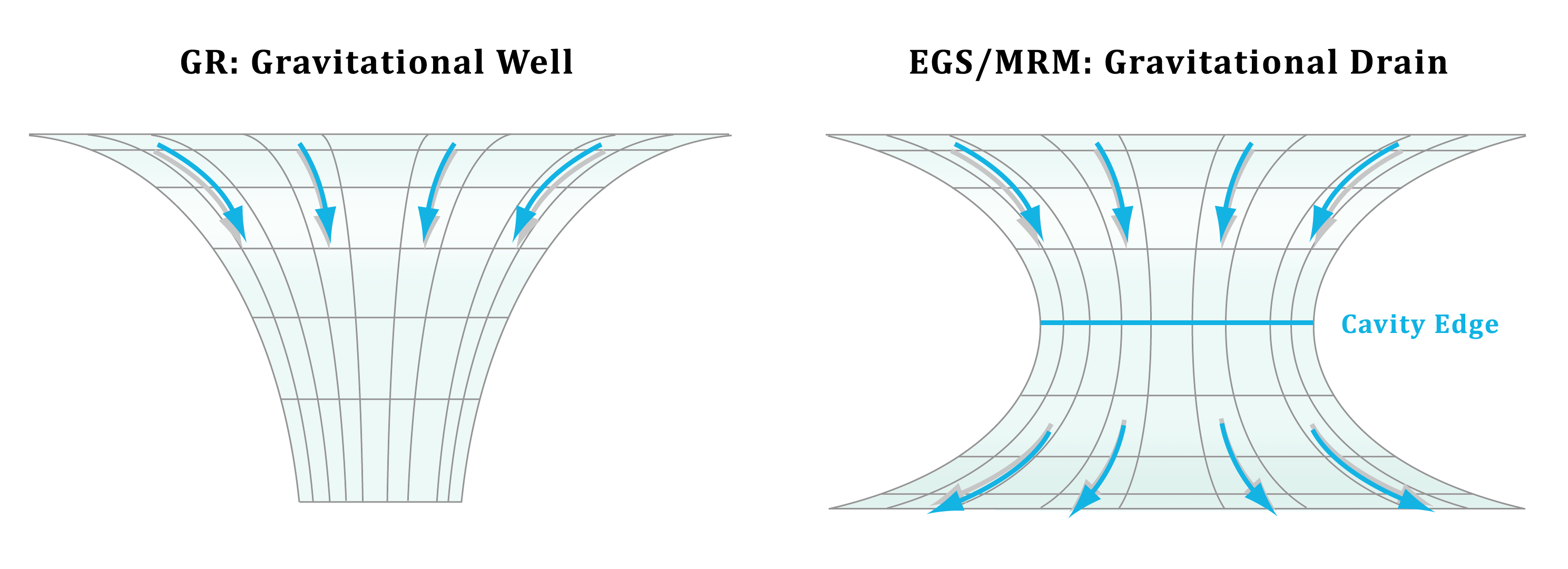
Interestingly, we can see that e^q also fulfills our expectations regarding the curvature of space. As the circumference according to the parent space decreases as a function of R, size contraction takes over at q=1 , the cavity edge. Objects that fall side by side into the gravitational system will appear to approach each other down to the cavity edge, and from that point, they will appear to expand away from each other.

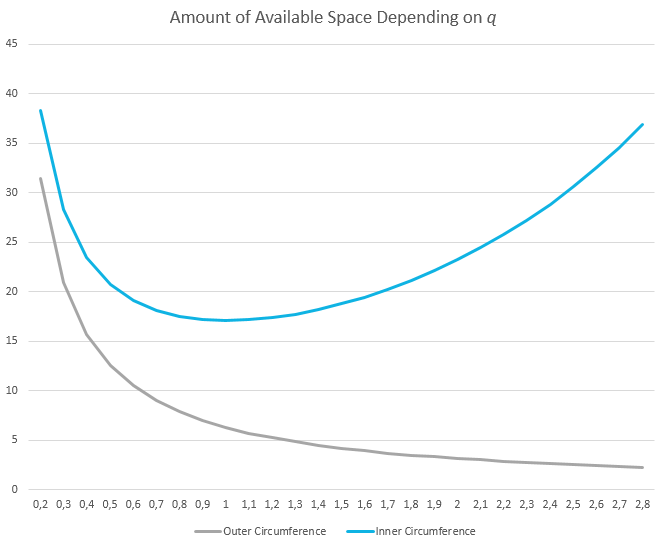
In contrast to the classic visualization of a gravitational well, in which objects are always are pulled toward a singular point, the EGS instead suggests something such a gravitational drain, in which the cavity edge represents a hole through which matter can flow. This visualization also illustrates why free momenta move in a perfect circle around the system at q=1 — they just follow the curvature of space.