3.7 Energy required for acceleration
The concepts of relativistic mass and rest mass are based on the assumption that γ in the formula for momentum, p=mγv, behaves as part of the factor m and is unrelated to the factor v.
However, when considering simulation charts, such as those presented in section 3.4 Mutual measurable relativistic effects, we rather get the impression that it is the other way around: An object being accelerated to a velocity of v will measure a proper velocity of γv when calculating its time of travel against objects in its original frame of reference. Additionally, if another object is accelerated to a speed of v, that frame of reference will be length contracted by a factor of γ. Even if we consider ourselves to be stationary, we must accept that we do indeed travel at a velocity of γv within the accelerated frame of reference.
The above observations suggest that in the formula for momentum, γ is associated with the factor v rather than with the factor m. In fact, relativistic momentum can be more easily understood if we free ourselves from the concept of relativistic mass. Before further progressing with this discussion, let us consider the formula for kinetic energy.
3.7.1 Verifying the formula for kinetic energy
It has already been demonstrated in many places on the Internet and throughout the literature how the formula for kinetic energy, Ek= mc2(γ-1), can be derived from the formula for momentum, p=mγv. We will not repeat this derivation here. Instead, we will see how the formula for kinetic energy can be theoretically verified.
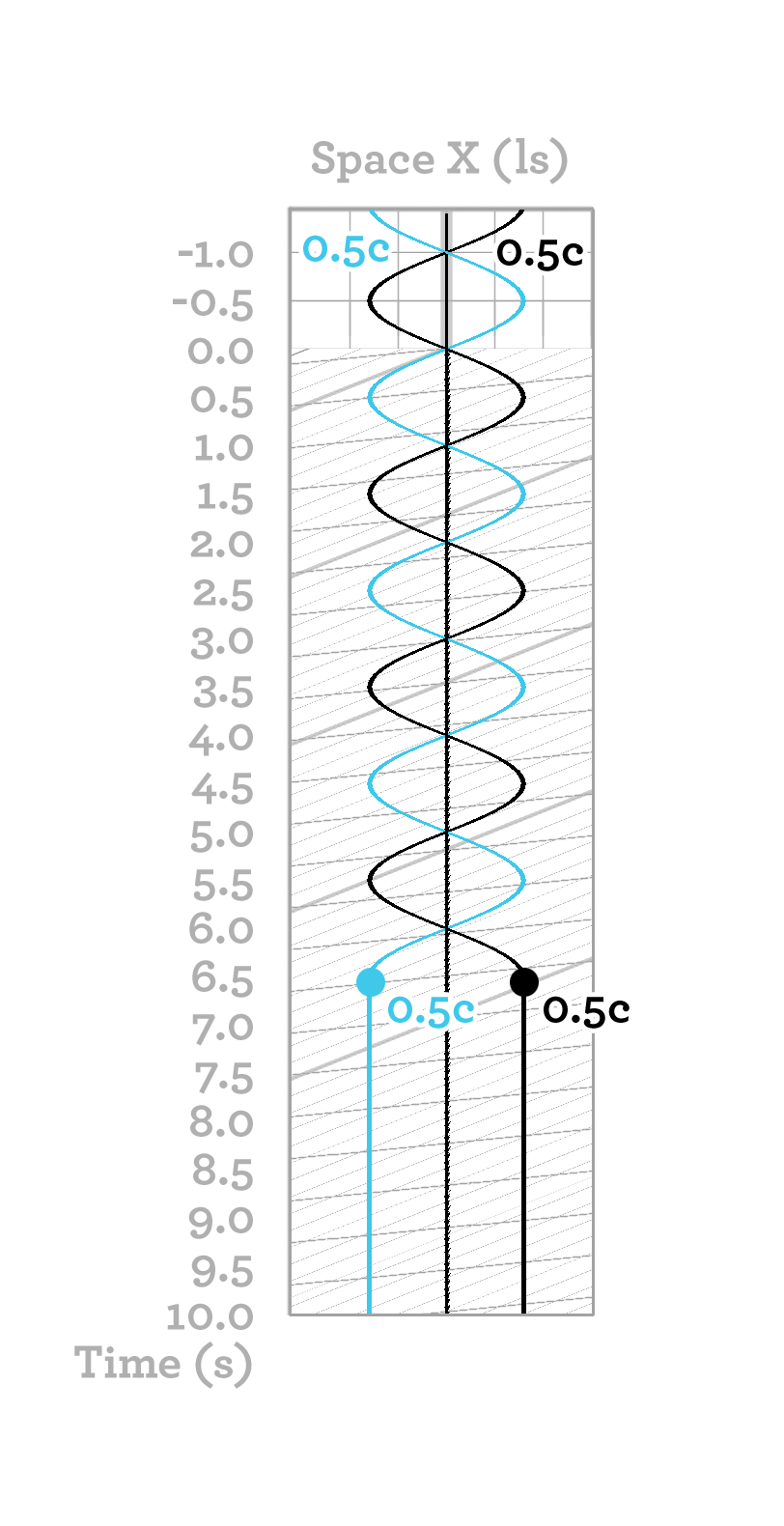
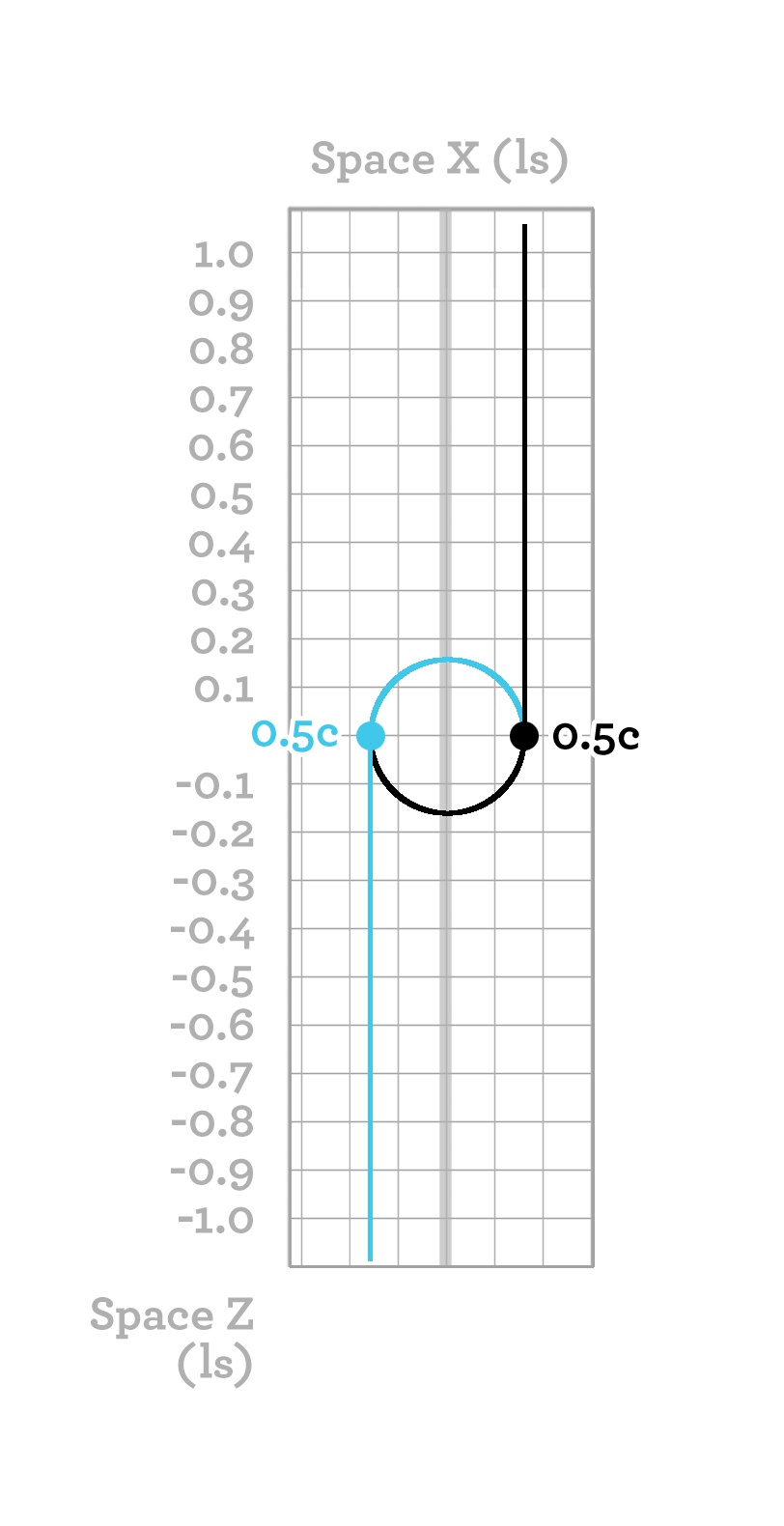
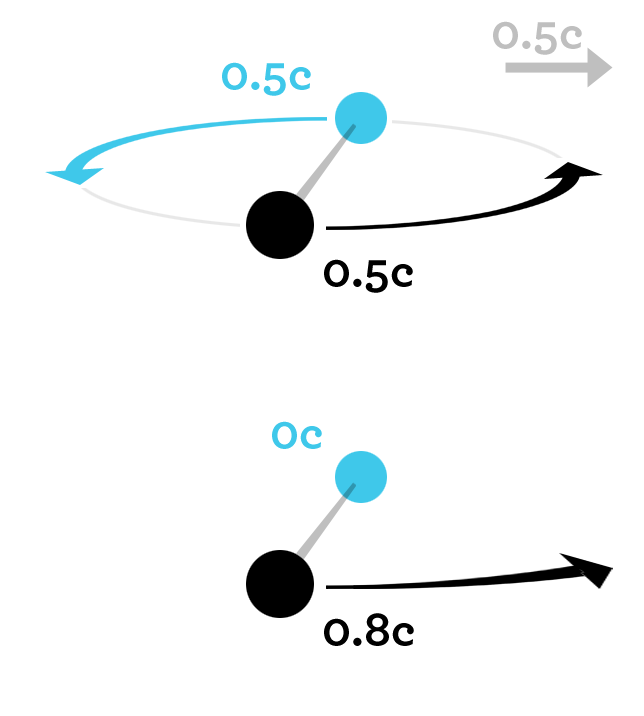Two objects with mass m are firmly attached to each other. They undergo frictionless rotation around each other at a speed of 0.5c. Now, we wish to accelerate this entire system to a speed of 0.5c. If we perform this boost when the objects are moving parallel to the direction of acceleration, we must cause one object (blue) to stand still and the other (black) to move at a speed of 0.8c. The result of 0.8c can be most easily calculated using rapidity. From the object we are immobilizing (blue), we can extract a kinetic energy of 0.1547mc2, as calculated from the formula for kinetic energy. The other object (black) also has a kinetic energy of 0.1547mc2, which should be increased to 0.66667mc2, the kinetic energy at 0.8c. The total amount of energy that we must add to the entire system is thus 0.66667mc2 - 0.1547mc2 - 0.1547mc2 = 0.35727mc2. If the two objects were stationary and we wished to accelerate them both to 0.5c, only 2 × 0.1547mc2 = 0.3094mc2 would be required.
Because the objects are rapidly rotating around each other, the entire system becomes more difficult to accelerate by a factor of 0.35727 / 0.3094 = 1.1547 => 15.47%.
How do we know that this result is correct? Let us turn to simulation charts to examine this scenario.
| Internal perception of movement |
External perception of movement |
| Front view | Front view |
 |
 |
| From above | From above |
 |
 |
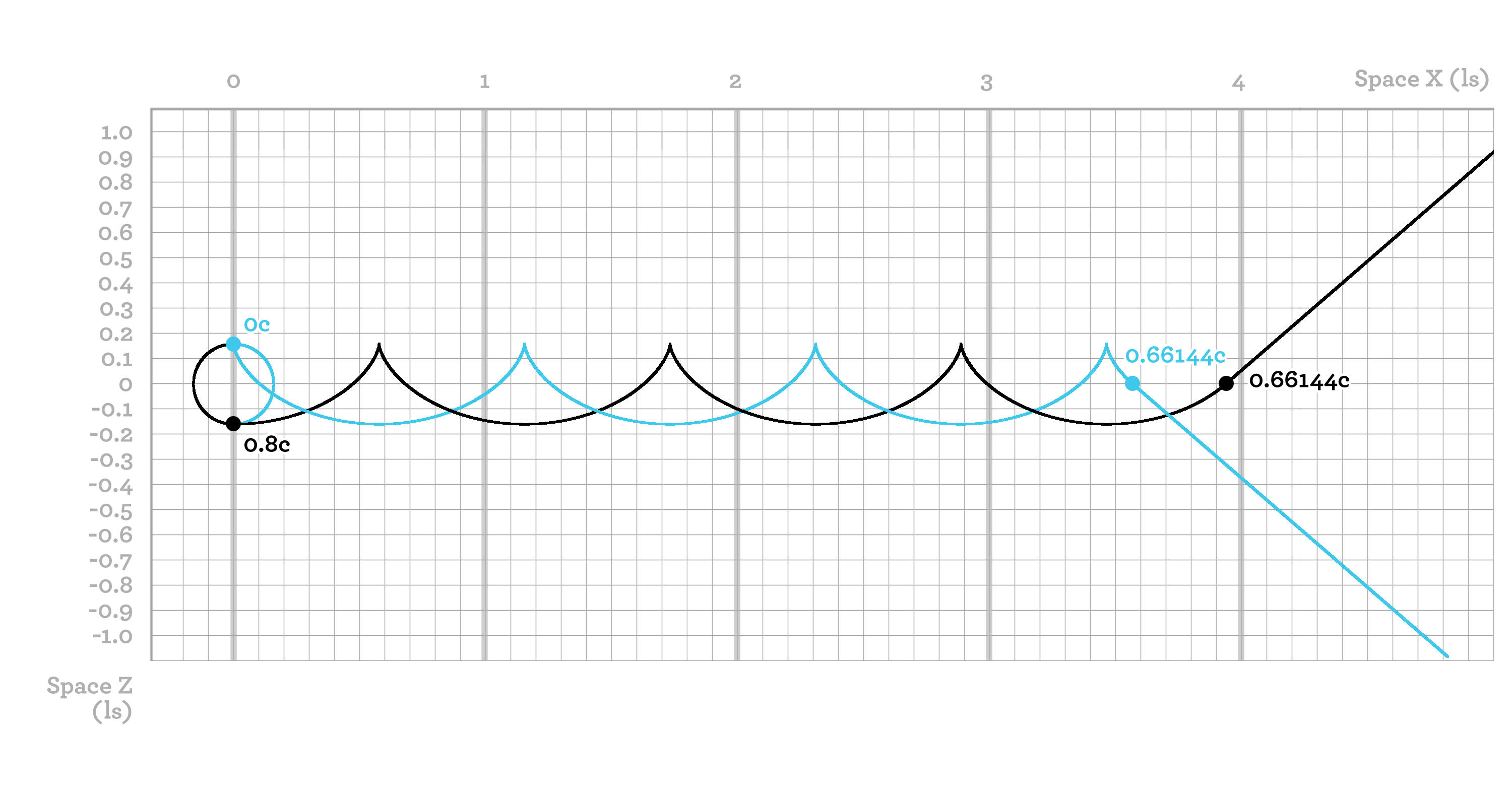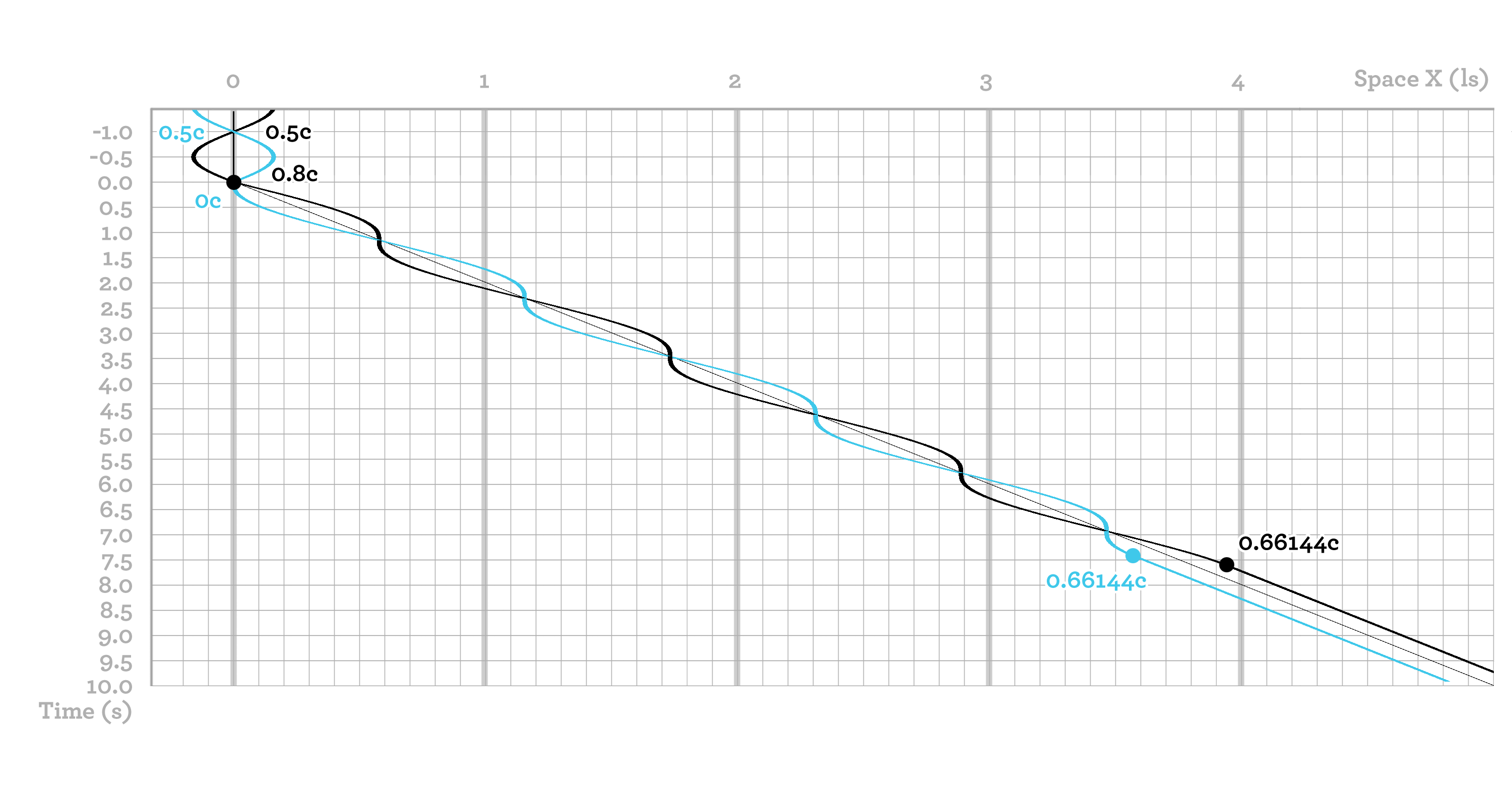
If the force that holds the two objects together is suddenly removed, they will stop rotating around each other. In such a case, the objects will simply continue along their current paths. It should be possible for this to occur at any point, and because of the conservation of energy, such an event must result in two objects that collectively possess exactly the same amount of kinetic energy that the entire system possessed when it was rotating. It is possible to show, through simulations or calculations using rapidity, that if the rotation is disrupted when the two objects are moving at an angle perpendicular to the movement of the entire system, according to the system itself, each of the two objects will gain a speed of 0.66144c. The kinetic energy for such a speed is 0.33333mc2, exactly half of the kinetic energy stored within the entire system.
It is possible to show that the formula Ek= mc2(γ-1) will produce two objects with a total sum energy of 0.66667mc2 regardless of when the objects are released from the rotation. Other methods of solution fail in this task. For instance, Ek=mφ2/2, a combination of rapidity and Newtonian mechanics, works very well for one-dimensional relativistic kinetic energy but fails when multiple dimensions are considered.