3.7 Energy required for acceleration
3.7.2 A clearer formulation
In the previous example, we note that what we interpret as mass, a resistance to acceleration, can be produced by internal kinetic energy. This theoretical observation leads us to conclude that all of the substance that we call �mass� actually consists of compounds of kinetic energy, or simply �energy�.
A more intuitive definition of mass would thus be to equate it to internal energy that manifests as a resistance to acceleration. The factors c and c2 that appear in various formulae for energy indicate a mismatch between the manner in which we measure energy and the manner in which we measure mass. To avoid this discrepancy, we can simply decide to use only energy and state that an object's internal energy relates to its mass as follows: Eint= mc2
What we now call the external kinetic energy can be calculated using Eext= Eint(γ-1)
We have also stated that relativistic momentum is attributable to a proper velocity. Let us define the proper velocity as u=γβ.
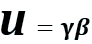
u is the proper velocity in units of c.
u is a universal variable, independent of the manner in which we choose to measure space and time. It is used throughout the description of the MRM to minimize the use of the human-defined constant c.
It should be noted that
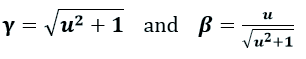
Let us also introduce a new definition of momentum, P = pc, to obtain clearer algebra by avoiding the human-defined concepts v and c.
We can now propose a generic definition of relativistic momentum: P = Eint u
The relation between external kinetic energy and momentum is thus
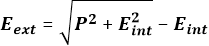
The external kinetic energy can also be expressed as follows
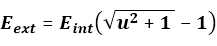
The total energy, including both internal and external energy, is thus
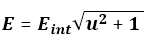
or simply E = Eint γ
For one single momenta, one single momentum vector, P = E.
These formulae are independent of which units we have used to specify energy E. The momentum P will adapt itself to this decision without requiring any change in the algebra.