3.1 The Internal Geometry Shift (IGS)

3.1.1 Identification

Do you believe that all objects with the same velocity will have a coherent geometry and appear to each other to be stationary? In other words, do you believe that objects can form new inertial frames of reference?

If you do, you must accept the fact that objects with different velocities must have different views of spatial geometry. When an object changes velocity, its perception of geometry must shift. This shift in geometry can be understood using a rather simple example.

Five planets are aligned in a row. The planets are not moving with respect to each other, and the distances between the planets are each a few light-minutes. Now, let us suppose that a spaceship is leaving each planet at the same time, in the same direction and at the same high speed.

Because of the distances between the planets, the ships' movements will be delayed with respect to each other.

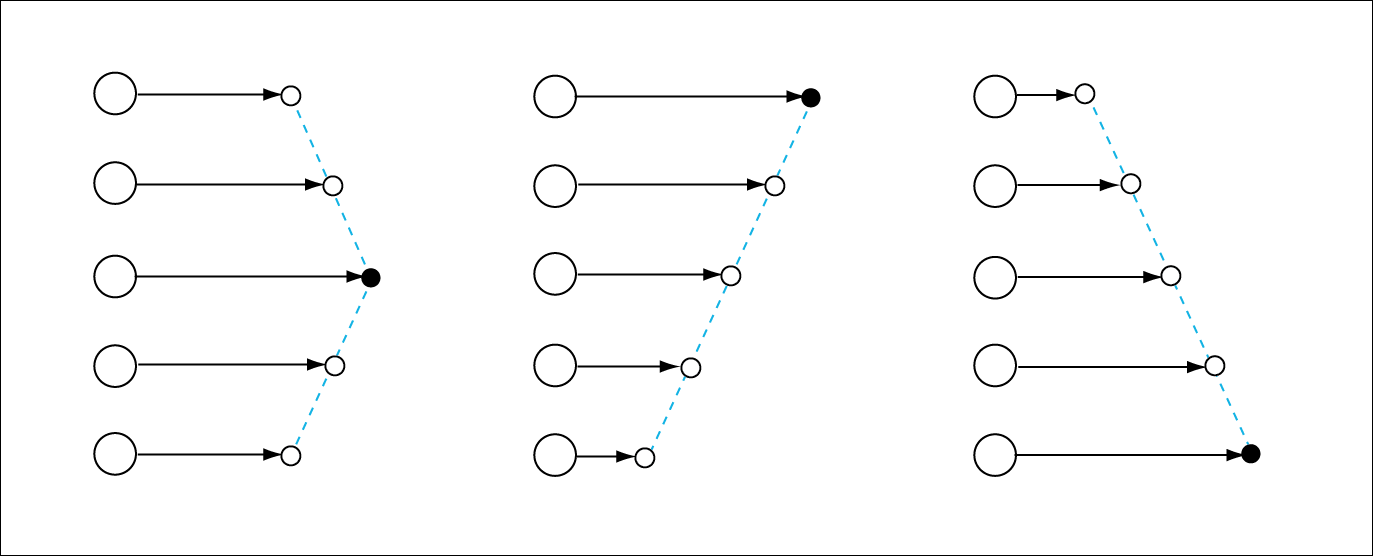
Figure 1. Spaceships leaving five planets as they would appear to each observer (black) after a certain amount of time without any shift in geometry.

As illustrated in Figure 1, the ships are traveling at the same speed and in the same direction, but they appear to have different opinions about their relative positions. Should the ships not form a straight line?

This problem cannot be solved by altering the moments when the ships are launched. If one ship is launched earlier, then from that ship�s perspective, all of the other ships will be delayed even more. Only a change in geometry can yield a straight line of ships and turn the planets into moving objects in their new frame of reference.

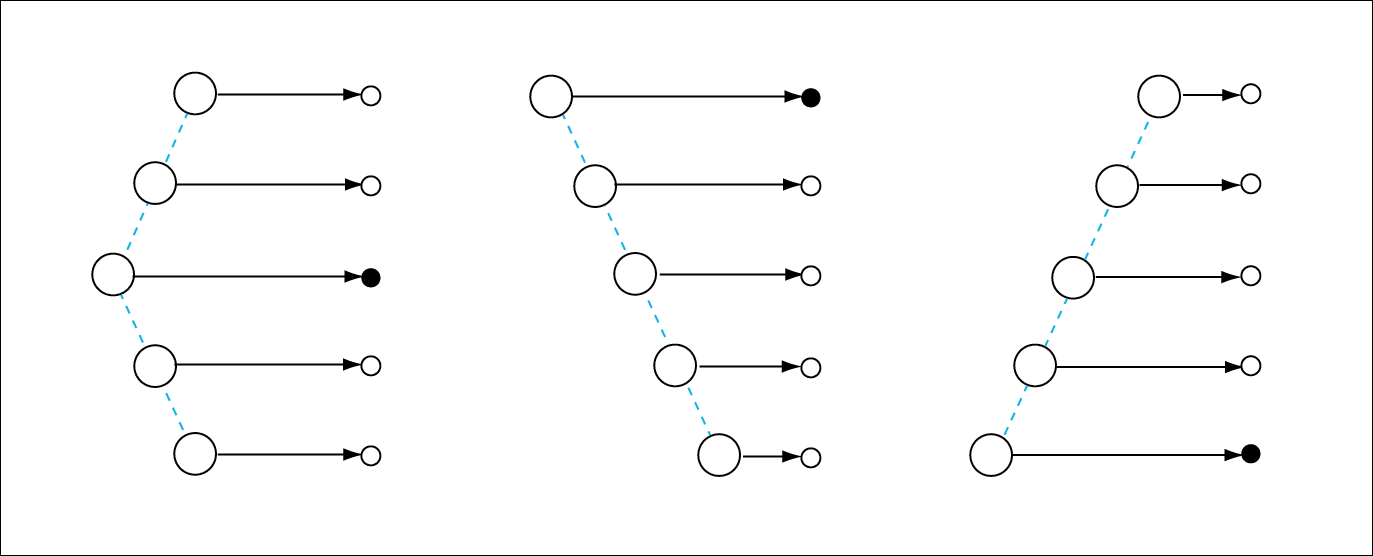
Figure 2. The planets' positions as they would appear to each observer (black) after a certain amount of time with a shift in geometry. (This drawing is a simplification. The formation of the planets would become more bow-like because of the shift. This image only illustrates the principle.)

One who regards light as particles might oppose this idea, saying that the straight line is formed by the additive speed being applied to these particles.

Let us consider the central ship and see what happens immediately after takeoff. At this point, we do not know whether the other planets are committed to the experiment. Will their ships launch? We will know this fact later, but at the moment, we do not. Still, we must adapt our view as we would expect the other ships to launch.

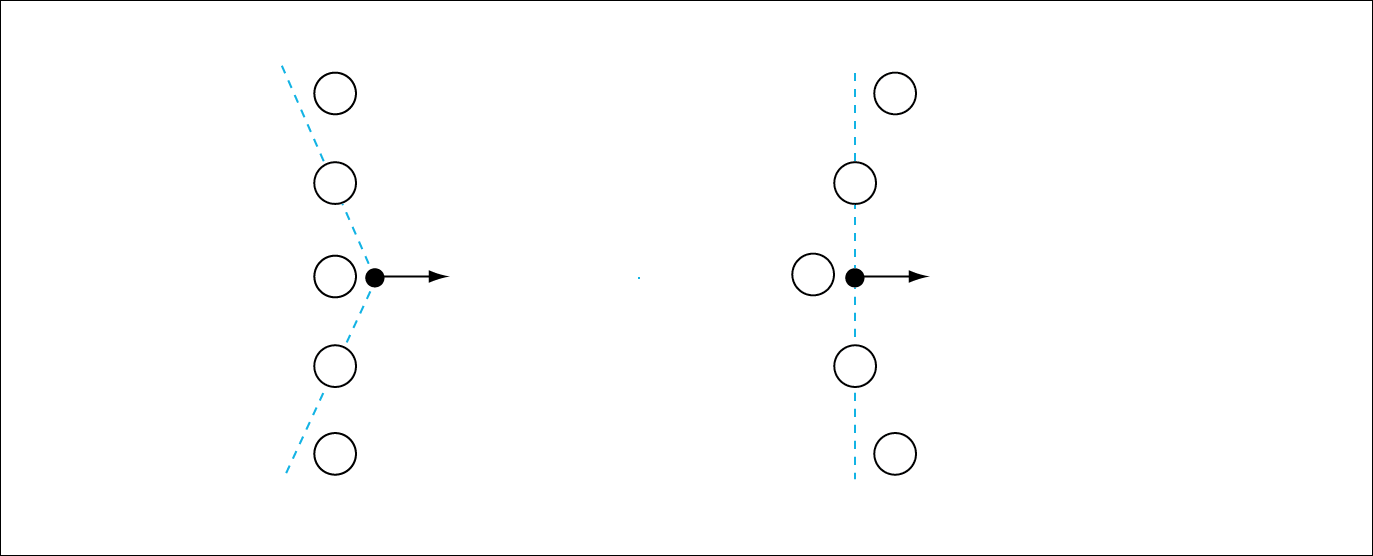
Figure 3. The midmost ship after takeoff as seen from the planets' frame of reference (left) and the ship's frame of reference (right).

As you can see, there are no moving objects that can emit the necessary light particles to describe a new straight line as an artifact of additive speed applied to light particles. We must accept that this shift is an immediate change in the perception of the spatial geometry. When an observer accelerates, his or her perception of a straight line must be tilted backward.

Let us now see what happens if we look forward and backward. We can use an example with 15 planets to examine this question.

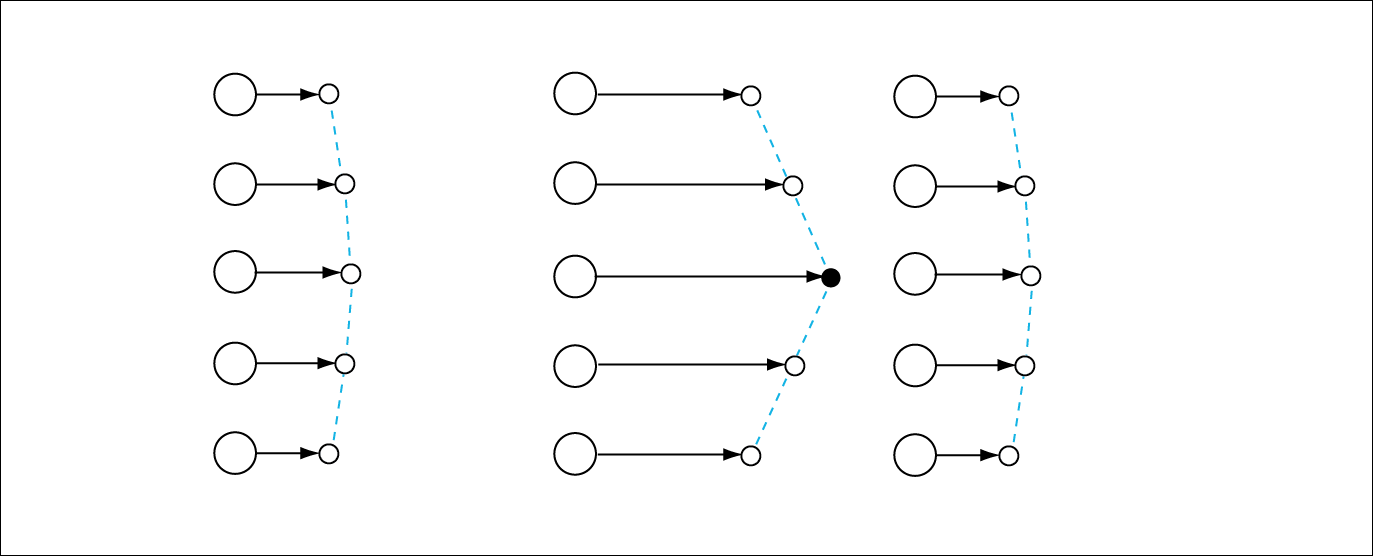
Figure 4. The situation as it would appear to the central ship (black) in a system with 15 planets after a certain amount of time without any shift in geometry.

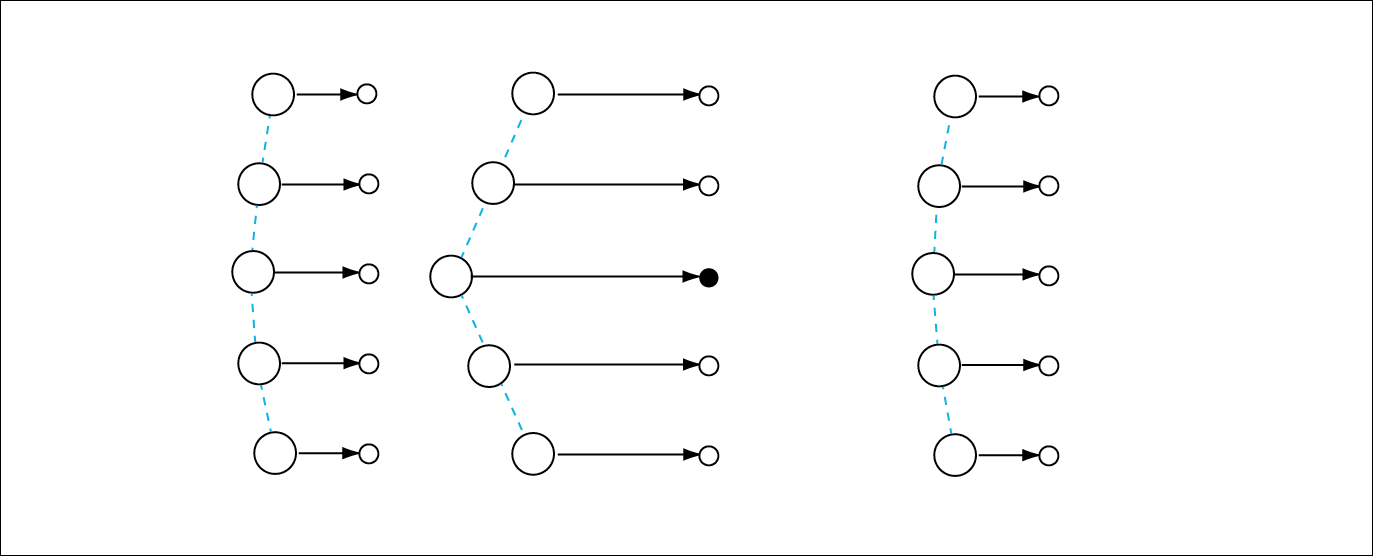
Figure 5. The situation as it would appear to the central ship in a system with 15 planets after a certain amount of time with a shift in geometry. (This drawing is a simplification because the shift itself will change the spatial delays over time. This image only illustrates the principle.)

If there are ships ahead or behind that are making the same alterations in speed, the IGS must ensure that all ships continue to agree on their relative distances. When one ship is speeding up, this shift leads to an expansion of the geometry ahead and to a contraction of the geometry behind. If the IGS did not exist, a situation would arise in which the ships disagreed on the distances between them, even though they were traveling at the same speed and in the same direction.