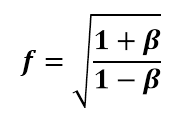3.1 The Internal Geometry Shift (IGS)

3.1.2 Deriving the expansion/contraction factor

For an accelerating observer, all distances straight ahead must be multiplied by the same factor (f) as that with which all distances straight behind are divided. Otherwise, spatial geometry will not be restored upon deceleration. All stationary objects in the previous frame of reference will also become moving objects in the new frame of reference and will appear to have the same ocular velocity to the observer that the observer appears to have to them. Using these two statements, we can obtain an equation for deriving the expansion/contraction factor (f) by imagining an object that is traveling a distance Δd, between, for example, planet A and planet B in section 2.2, and the resultant times must match when looking both ahead and behind.

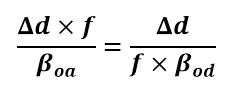
where

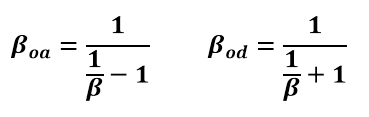
These expressions are easily converted into the following:

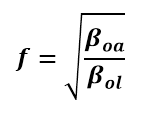
β is the measured velocity in units of c according to the outer frame of reference, which is the frame of reference that we wish to transform. f is the factor by which all distances straight ahead should be multiplied. The same factor f should be used to divide all distances straight behind. The equation can also be written as