3.1 The Internal Geometry Shift (IGS)

3.1.4 Deriving the full IGS transformation

To derive the full transformation formula for the IGS, we can use the expansion/contraction factor and the illustrations on the previous page. The use of circles and ellipses is very accurate because it will not bend the geometry, meaning that the observer will not become able to see around objects simply because he or she changes velocity. Such an effect is unreasonable. It is also apparent that the positions are only shifted along the axis of travel, i.e., if the object has a relative velocity along the x axis, there will be no changes in the positions along the y or z axes. Changes in these axes would lead to unreasonable results during acceleration and deceleration.

We can see that there is a stretch and an offset. The stretch determines how much the axis is expanding, and the offset determines the displacement of the ellipse of which the object is a part. Based on these observations, we can construct the following equations:

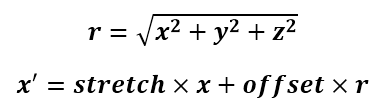
where

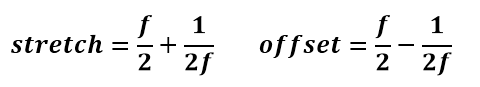
Stretch is the total stretch when looking both ahead and behind. Offset is the new center of the ellipse of which the object is a part. Inserting the equation for f as a function of β into these equations leads, after simplification, to

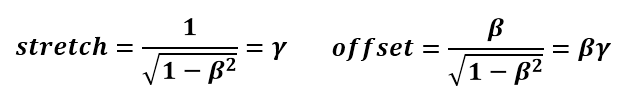
The stretch is apparently the Lorentz factor. The offset is the measured velocity according to the outer frame of reference multiplied by the Lorentz factor. Thus, the final formula is

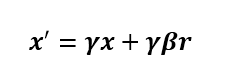
We can verify the symmetry of the formula by entering test values into it. It should be possible to reinsert resulting x' as a negative number to obtain a negative version of the original number. Inserting β=0.5, x=100, y=50 and z=0 will result in x'=180, and inserting β=0.5, x=-180, y=50 and z=1 will result in x'=-100. It is also possible to reinsert the new x' and the negative velocity to obtain the positive equivalent of the original x: β=-0.5, x=180, y=50 and z=1 will result in x'=100. The formula is truly symmetrical. To calculate transformations in other directions, it is easiest to first rotate the axis, perform the calculation and then rotate the result. Two objects can have only one relative direction of movement.

Using the IGS transformation, we can visualize the immediate changes in the perception of geometry that arise with a change in velocity.